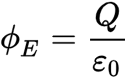Magnetic Flux is a key concept in the field of Electromagnetism, and the topic which I’ll be trying to explain in this post. Whilst confusing for many, I’ll do my best to explain in a simple, digestible manner so that you can grasp the concept, and understand concepts related to it with more ease.
Magnetic Flux
Magnetic Flux is a term which explains how much of a Magnetic Field flows through a given area. If we imagine a Magnetic Field to be a hose, then the Magnetic Flux would be the area that the hose’s water cleans.
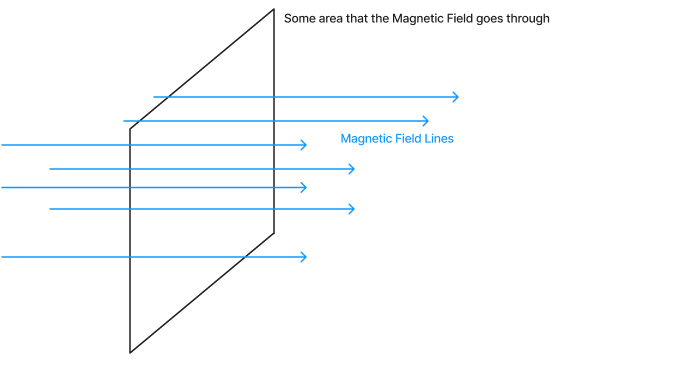
When we draw diagrams for Magnetic Fields, we represent the field itself with lines that move from the North Pole to the South Pole, and we have some wall/area that we measure to determine the Magnetic Flux.
The formula for the Magnetic Flux is: ΦB (Magnetic Flux) = BAcosθ. Let’s break this down.
B here represents the Magnetic Field (which I’ll explain how to calculate in another post) measured in a unit of Teslas, with A being the enclosed area, which here is the area of our square wall. You can think of this section. as B being the Field Lines, and A the square/surface that the Field Lines go through.
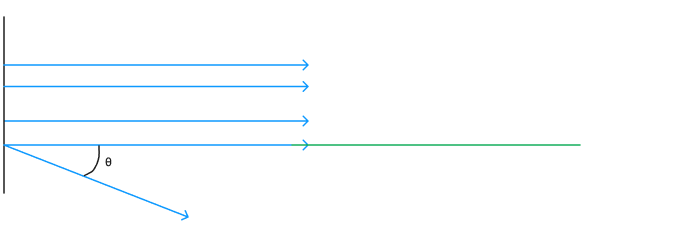
Now, the thing that may confuse some people would be the cosθ part, and for those who are confused, we’ll need to take a different look at the above diagram:
This diagram represents the same thing as the previous diagram but is a side view, and we have a Green Line here as a reference point, to represent the direction of a Magnetic Field if it were perpendicular (at 90 degrees) to the area which the Magnetic Field passes through.
The main reason we look at it this way is to show what we mean by θ, where if the Magnetic Field Lines are perpendicular to our area, then they’ll be parallel to our reference line, which would give our cosθ its maximum value. The gist of it is that as our Magnetic Field bends, so as θ increases, so as the angle between our field lines and reference lines increases, the magnitude of our Magnetic Flux would reduce.
Gauss’s Law
Gauss’s law talks about the Electric Flux that goes through some area on a 3D object. If we had a sphere, and we marked some area out by drawing a circle at some point, then we’d say that Gauss’s law would measure the Magnetic Flux going through that area.
Here, we introduce a new symbol: ε0, which stands for the “Permittivity of Freespace”. It’s a confusing idea, but simply put: It’s a constant that tells us how well a Magnetic Field could travel through a Vacuum → We don’t need to overthink this, since it’s a constant (just a number: It doesn’t change).
Q is a measure of the total charge that exists in this 3D object. If we had a box containing 50 electrons (just as an example), then Q would be the same as the Total Charge of 50 Electrons.
The key point of this law is that the Total Electric Charge that’s enclosed in a surface will lead to an increase in Magnetic Flux, which adds to what we mentioned a while ago: Electric and Magnetic Fields are related.
However, this is not Gauss’s only laws that explore how Electric and Magnetic Fields are related. There are two more equations, which are used in Maxwell’s Equations, which are the main equations that relate Electric and Magnetic Fields.
To recap, we’ve covered:
What Magnetic Flux is, and how to calculate the Magnetic Flux.
Gauss’s Law, explains how Magnetic Flux is related to the Total Charge of the 3D object.